在某些資料中，隨著滾動，俯仰和偏航的應用順序的重要性不斷發生。但是我不明白為什麼這是相關的。
握住右手：將拇指向上，食指遠離您，中指向左。現在您有了一個右手坐標系：您的拇指是x軸，食指是y軸，中指是z軸。
首先圍繞x軸（拇指）旋轉+ 90°。現在，食指指向左側，中指指向您。接下來，繞y軸（食指）旋轉+ 90°。現在，拇指指向遠離您的位置，食指指向左側，中指指向上方。
現在，移回初始位置，並以不同的順序應用相同的兩次旋轉，首先圍繞y軸，然後是x軸：圍繞y軸（食指）旋轉+ 90°。您的拇指現在指向右，食指遠離您，中指向上。接下來，繞x軸（拇指）旋轉+ 90°。現在，您的拇指指向右，食指向上，中指指向您。
這與上一個結果不同：旋轉順序很重要。
我通過將加速度計值輸入到互聯網上的一些公式中來使用加速度計值（那些反正切公式，每個人都使用，但是沒人能很好解釋）
當飛機以恆定速度運動時，加速度計只是測量由於重力引起的加速度，重力是在全局坐標系中正好指向下方的向量（0，0，-g）。無論傳感器的方向如何，這始終是正確的。
如果傳感器處於水平位置，則傳感器的局部坐標係與全局坐標係對齊，因此傳感器也將測量（0，0，-g）。
當傳感器傾斜時，被測矢量還具有x和y分量。
為簡單起見，假設傳感器圍繞y軸正軸傾斜。
傳感器現在測量x分量和z分量：（x，0，-z）。
從下圖中可以看到，旋轉角度θ= atan2（x，z）。
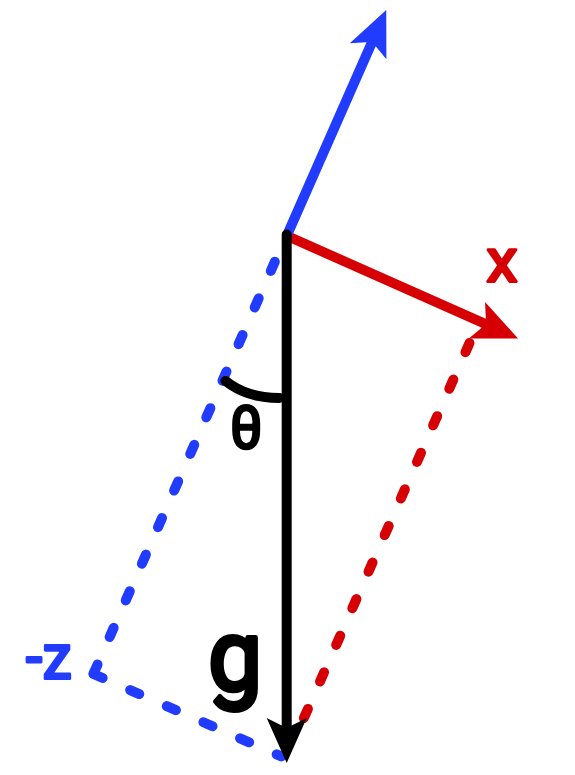黑色箭頭是重力引起的加速度，
但是，加速度傳感器的測量值對於確定傳感器在加速時的方向沒有用，因為陀螺儀可以測量角速度，因為那樣一來，測量的矢量就不再精確指向下方（在全局坐標系中）。
陀螺儀測量角速度。通過積分角速度，您可以獲得角度。
有一個警告：不可能精確積分，因為我們僅在離散的時間點進行測量。這意味著我們必須使用類似於Euler方法的方法，已知該方法會導致方向估計值的漂移。更糟糕的是，測量噪聲很大，而且噪聲也被積分，從而導致更大的誤差。
幸運的是，您可以使用傳感器將兩個不完美的測量合併為一個更好的方向估計值融合算法。我已經成功地將 Sebastian Madgwick的算法用於我的四軸飛行器。
它使用加速度計的測量值來最小化陀螺儀的漂移。
請注意，該算法使用四元數代替了Euler。角度（橫搖，俯仰，偏航），因為後者受常平架鎖定，並且由於四元數通常需要較少的處理能力。
還請注意，您無法使用加速度計確定偏航角，因此
使用四元數進行所有計算是一個好主意。您的四軸飛行器可能不需要歐拉角，除非出於調試目的。
如果願意，還可以直接從加速度矢量獲取四元數：
四元數quaternionFromDirection（Vec3f v）{/ * *公式：* q = cos（ϑ / 2）+ sin（ϑ / 2）·（x·i + y·j + z·k）*其中（xyz）是代表*物體圍繞的軸的單位矢量旋轉ϑ是旋轉角度。 * *來源：* https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation#Using_quaternion_as_rotations * *旋轉軸（x y z）可以通過取（0 0 1）和給定矢量的歸一乘積來計算。旋轉角度* using可以使用| A×B |找到。 = | A || B |·sin（ϑ）。 * / //首先檢查邊緣情況，其中v ==（0 0 z），即垂直if（v.x == 0 && v.y == 0）返回{1，0，0，0}; //計算叉積及其範數。 Vec3f cross = {v.y，-v.x，0}; float crossNorm = cross.norm（）;交叉/ = crossNorm; //計算角度ϑ。浮角= std :: asin（crossNorm / v.norm（））; //計算所得的四元數。 return {std :: cos（angle / 2），// std :: sin（angle / 2）* cross.x，// std :: sin（angle / 2）* cross.y，// std :: sin （angle / 2）* cross.z，//}; }